本文是我在上UCSD的 CSE 120: Principles of Operating Systems (Winter 2020) 整理的笔记,这一课主要介绍了操作系统里面逻辑内存的概念,包括页(page)和段(segment)的概念和实现。
Introduction
Definition
- Logical memory = a process’s memory
- As viewed (referenced) by a process
- Allocated without regard to physical memory
Problems with sharing memory
The addressing problem
- Compiler generates memory reference
- Unknown where process will be located
The protection problem
- Modifying another process’s memory
The space problem
- The more processes there are, the less memory each individually can have
Logical vs. Physical Addressing
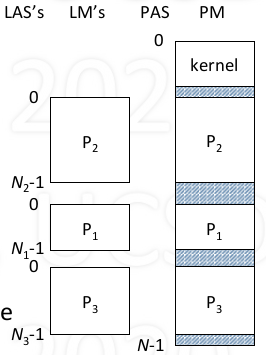
Logical addresses
- Assumes seperate memory starting at 0
- Compiler generated
- Independent of location in physical memory
Convert logical to physical
- Via software: at load time
- Via hardware: at access time
Hardware for Logical addressing
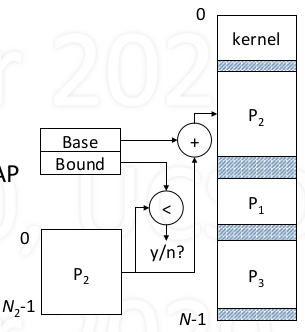
- Base register filled with start address
- To translate logical address, add base
- Achieves relocation
- To more process: change base
Protection
- Bound register works with base register
Is address < bound
- Yes: add to base
- No: invalid address, TRAP
Achieves protection
Memory Registers are part of context
On every context switch
- Load base/bound register for selected process
- Only kernel does loading of these register
- Kernel must be proetced from all processes
Benefit
- Allows each proces to be seperated located
- Protecs each process from all others
Process mempory allocation
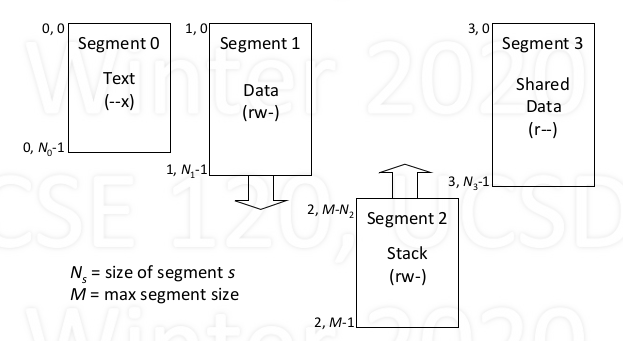
Process address space
Text: program instruction
- excute-only, fixed size
Data: varaible (static, heap)
- read/write, variable size
- dynamic allocation by request
Stack: activation records, local variable
- read/write, varibale size
- Automatic growth/shrinkage
Fitting process into memory
- Must find large enough hole
- May not succeed even if enought fragment space
- Even successul, it’s inefficient since space must be allocated for potential growth area
Solution: break process into pieces
- Distribute into available holes
- Two approaches: Segment and Page
Segementation
Segemented Address Space
- Address space is a set of segments
Segment: a linearly addressed memory
- Typically contains logically-related information
- Examples: program code, data, stack
Each segment has an identifier s, and a size N
- s between 0 and S-1, S = max number of segments
Logical addresses are of the form (s, i)
- offset i within segment s, i must be less than N
Example
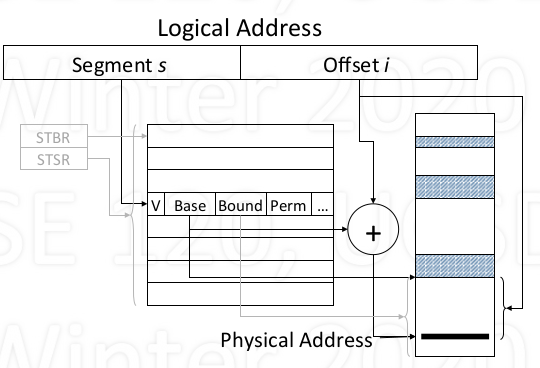
Segment-based address translation
- Problem: how to translate a logical address (s, i) into physical address a?
Solution: use a segment (translate) table (ST)
- to segment s into base physical address b = ST(s)
- then add b and i
physical address a = ST(s) + i
Segment Table
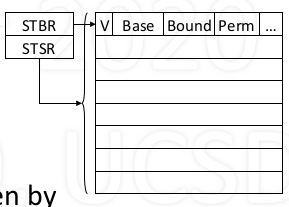
- One table per process (typically)
Table entry elements
- V: valid bit
- Base: segment location
- Bound: segment size
- Perm: permissions
Location in memory given by
- Segment table base register(hardware)
- Segment table size register(hardware)
Address translation
- physical address a = base of s + i
do a series of checks
- s < STSR? -> is segment identifier valid or not?
- V == 1? -> the corresponding entry is valid?
- i < Bound? -> logical address is out of bound?
- Perm(op) -> that block has required operation(r/w/x)?
Then access that physical address
Sizing the segment table
Given 32 bit logical, 1 GB physical memory (max)
- 5 bit segment number, 27 bit offset
Logical address
Segement s: number of bits n specifies maxsize of table, where number of entries = $2^n$
- if 32 entries, n = 5
Offset i: number of bits n specifies maxsize of segment
- 27 bits needed to size up to 128MB
segment table
- V: 1 bit
Base: number of bits needed to address physical memory
- 30 bits needed to address 1GB
Bound: number of bits needed to specify max segment size
- 27 bits needed to size up to 128MB
Perm: assume 3 bit (r/w/x)
one entry: $1 + 30 + 27 + 3 + … = 61$+ bits $\approx$ 8 bytes
- whole table: 32 * 8 = 256 bytes
Pros and Cons
Pros: Each segment can be
- located independently
- seperately protected
- grown/shrunk independently
- Segments can be shared by processes (via segment table)
Cons: Variable-size allocation
- Difficult to find holes in physical memory
- External fragmentation
Paging
Paged Address Space
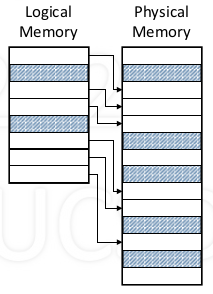
Logical (process) memory
- Linear sequence of pages
Physical memory
- Linear sequence of frames
Pages and frames
- Frame: a physical unit of information
- A page fits exactly into a frame
- Fixed size, all pages/frames same size
Page-based Logical Addressing
Form of logical address: (p, i)
- p is page number, 0 to N - 1
- i is offset within page, since page size is fixed, i is guaranteed to be less than page size, no need to check
Size of logical address space
- $N_L$ = max number of pages
- $N_L \times$ page size = size of logical address space
Frame-based Physical Addressing
Form of physical address: (f, i)
- f is frame number, 0 to N - 1
- i is offset within frame, less than frame size
Size of physical address space
- $N_p$ = max number of frames
- $N_p \times$ frame size = size of physical address space
Page-based address translation
- Problem: how to translate logical address (p, i) into physical address (f, i)
Solution: use a page (translation) table PT
- translate page p into frame f = PT(p)
- then concatenate f and i
Physical address (f, i) = PT(p) || i = (PT(p), i)
Page table
- Each page of logical memory correspondings to entry in page table
- Page table maps logical page into frame of physical memory
- One table per process (typically)
Table entry elements
- V: valid bit
- DPB: demand paging bits
- Frame: page location
Location in memory given by
- Page table base register(PTBR) (hardware)
- Page table size register(PTSR) (hardware)
Address translation
- Physical address = frame of p || offset i
Do a series of checks (similar to segmenatation)
- p < PTSR?
- V == 1?
- Perm(op)?
Sizing the page table
Given 32 bit logical, 1 GB physical memory (max)
- 20 bit page number, 12 bit offset
Logical address
- page p: 20 bits to address $2^{20} =$ 1M entries
- offset i: 12 bits, page size = frame size = $2^{12} =$ 4096 bytes.
Page table
- V: 1 bit
- DPB: 3 bits
- Frame: 18 bits to address $2^{30}/2^{12}$ frames
- Perm: 3bits
- One entry: $1+3+18+3+…= 25$+ bits $\approx$ 4 bytes
- Whole table size = 1M * 4 = 4 MB
Address translation
Segments vs. Pages
Segment is good “logical” unit of information
- Can be sized to fit any contents
- Makes sense to share (e.g., code, data)
- Can be protected according to contents
Page is good “physical” unit of information
- Simple memory management
Combining segments and pages
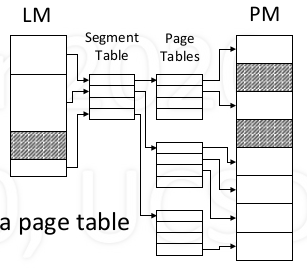
Logical memory
- composed of segments
Each segment
- composed of pages
Segment table
- Maps each segment to a page table
Page tables
- Maps each page to physical page frames
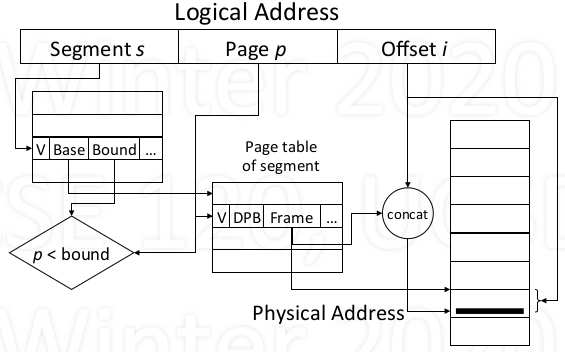
Address Translation
- Logical address: [segment s, page p, offset i]
Do various checks
- s < STSR, V == 1, p < bound, perm(op)
- May get a segmentation violation
Use s to index segment table to get page table
- Use p to index page table to get frame f
Physical address = concatenate (f, i)
More on addressing
Cost of translation
Each lookup costs another memory reference
- For each reference, additional references required
- Slows machine down by factor of 2 or more
Take advantage of locality of reference
- Most references are to a small number of pages
- Keep translation of these in high-speed memory
Problem: don’t know which pages till accessed
Translation Look-aside Buffer (TLB)
- Fast memory keeps most recent translations
- If key matches, get frame number
else wait for normal translation (in parallel)
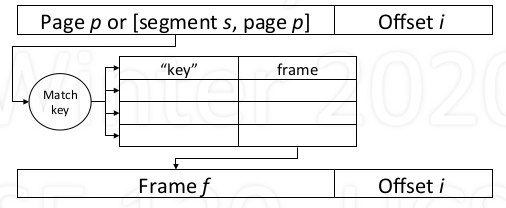
Translation Cost with TLB
Cost is determined by
- Speed of memory: ~100 nsec
- Speed of TLB: ~5 nsec
- Hit ratio: fraction of refs satisfied by TLB, ~99%
Speed with no address translation: 100 nsec
Speed with address translation
- TLB miss: 200 nsec (100% slowdown)
- TLB hit: 105 nsec (5% slowdown)
- Average: 105 x 0.99 + 200 x 0.01 ~ 106 nsec
TLB Design Issues
The larger the TLB
- the higher the hit rate
- the slower the reponse
- the greater the expense
TLB has a major effect on performance!
- Must be flushed on context switched
- Alternative: tagging entries with PIDs