激光雷达运动畸变去除

本文是我在学习深蓝学院的激光slam课程第三讲的学习笔记，在上一节课学习了轮式里程计的校正之后，这一课学习传感器数据预处理的另一部分：激光雷达运动畸变的校正，这一部分是对激光slam的效果和性能影响非常大的部分。这篇大部分的公式推导并不困难，主要在理解不同方法的要点和思想以及优缺点。

激光雷达

传感器介绍

按照测距原理分激光雷达有两种

三角测距

三角测距的大致原理如下图所示，和双目类似通过两个点测出目标点和两点连线的距离，计算方法大概如下：

$$\begin{aligned} x + y &= L \\ \frac{x}{\sin{(\frac{\pi}{2}-\beta)}} &= \frac{d}{\sin{\beta}} \\ \frac{y}{\sin{(\frac{\pi}{2}-\alpha)}} &= \frac{d}{\sin{\alpha}} \end{aligned}$$

三个方程三个未知数，联立可以解出，可以发现距离和基线和两个出射角都有关：

$$d = L \frac{\sin{\alpha}\sin{\beta}}{\sin{(\alpha+\beta)}}$$

三角测距有以下特点：

• 受限于基线长度，中近距离精度较高，远距离精度较差（所以一般在室内用）
• 结构简单，价格比较便宜
• 比较容易受干扰（强光等）

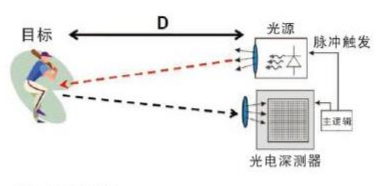
飞行时间测距（tof）

飞行时间的测距原理如下所示，原理偏光学一点所以不推导了。

TOF的特点：

• 测距范围广（只跟时间差/光相位差有关，距离影响不大）
• 测距精度高
• 抗干扰能力强
• 价格贵
• 室内/外都可以用

激光雷达数学模型介绍

这里主要介绍如何通过激光束的观测结果以及地图来计算机器人位姿的数学模型。

光束模型（beam model）

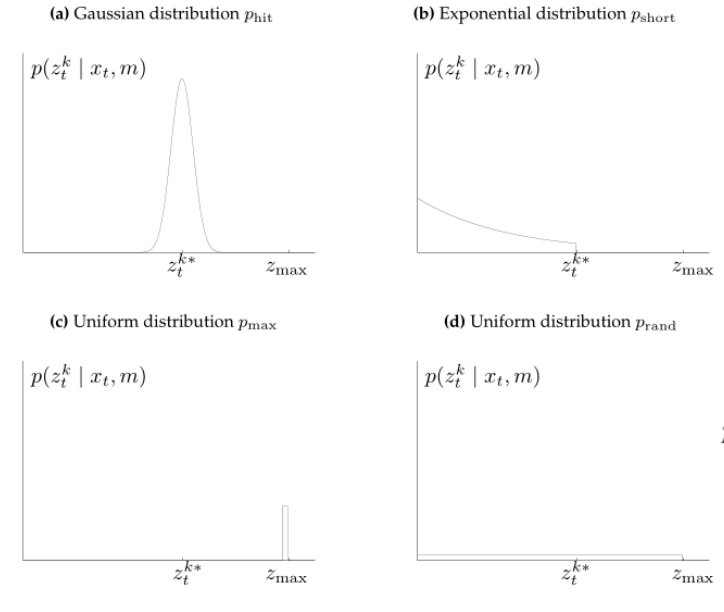
这个模型是概率学提出的比较传统的数学模型，具体来说可以参考以下四张图。假设机器人位姿是 $x_t$, 并且发射一束激光期望能够打到前方 $z_t^*$ (期望值)距离处的物体（根据地图 $m$ 获得期望值），但是由于各种原因（噪声），返回来的值 $z_t$ (观测值)不一定和实际值一致。而光束模型认为总共能有四种噪声和真实值耦合形成观测值，分别是：

• 高斯噪声：高斯噪声使得观测值在真实值周围形成高斯分布 （大部分时候是符合这个分布）
• 物体被遮挡：因为物体被遮挡所以观测值会比真实值小很多，形成指数分布 （出现动态物体的时候会出现）
• 没扫到物体：因为物体没被扫到所以观测值无穷大（可以通过判断是否超出有效距离过滤掉）
• 均匀噪声：均匀噪声使得观测值在真实值周围形成均匀分布（正常传感器应该不太会出现这种噪声）

基于这四种模型，我们给每种模型分配不同的权重(对每一个激光点 $z_t^k$， 共k个)计算出在当前位姿基于建好的地图出现观测值的概率就可以用来判断位姿的准确性，计算过程如下：
先计算出每个激光点的得分（出现概率，越高所以越准确），第一项是四个模型的权重，一般高斯分布的权重会比较高（大部分），均匀分布的权重比较低（出现情况很少）。

$$p(z_t^k|x_t, m) = \begin{bmatrix}z_{hit}\\z_{short}\\z_{max}\\z_{rand}\end{bmatrix}^T\begin{bmatrix}p_{hit}(z_t^k|x_t,m)\\p_{short}(z_t^k|x_t,m)\\p_{max}(z_t^k|x_t,m)\\p_{rand}(z_t^k|x_t,m)\end{bmatrix}$$

然后我们再把该帧所有激光点的概率相乘就能得到这帧激光束的得分（概率），这个模型的要点就要搜索一个位姿 $x_t^*$ 使得该帧的得分（出现概率）最高。

$$p(z_t|x_t, m) = \prod_{k=1}^Kp(z_t^k|x_t, m)$$

这个模型需要将一个激光束中所有的点的概率都计算出来（一条线上的所有激光点）而且一帧有很多条激光束，计算量大。
并且这个模型有一个致命的缺点。假设我们考虑在一个比较结构化的场景（室内环境，大部分都是平面的结构等等）的时候，这个时候当我们在靠近真实值的过程中，我们可以发现计算出来的激光束的得分是逐渐上升的，而且变化大部分是一个连续的过程，这种场景下没有问题。但是如果在比较不规则的场景（室外环境，假设有一个电线杆在 $z_t^$ 处），这个时候只要我们*假设的位姿离真实位姿有一点点的变化都会导致激光束的得分急剧降低（只要稍微旋转一下就扫不动电线杆，所以会出现无穷大 $z_{max}$ ，而实际激光束 $z_t$ 并不是），所以这会给搜索带来很大的困难以及误匹配，因为这两个原因，所以现在实际上比较少采用这种模型。

似然场模型 (likelyhood model)

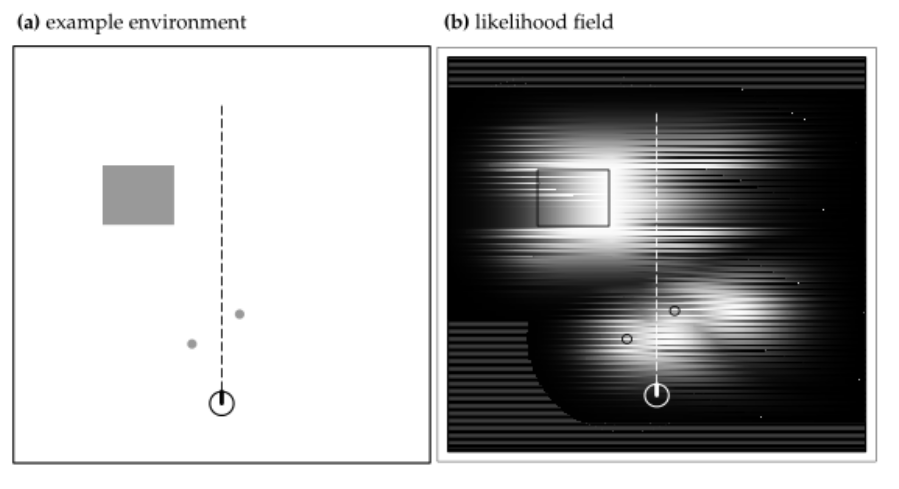
似然场模型的原理如下图所示，左边是实际环境图 $m$ ，这个时候如果不考虑似然场的话我们可以认为如果在给定位姿 $x_t$ 的时候打中 实际障碍物的概率是 1，如果没打中就是 0，这样每条激光束出现概率非 0 即 1，过于绝对出现光束模型的病态问题，似然场模型的要点是将地图进行高斯平滑，激光束击中障碍物周围的环境形成以障碍物位姿为中心的高斯分布，这样就算我们估算的位姿不是很准确导致在那个位姿实际上打不到障碍物，如右图所示，该帧观测值的概率也不会是0，而是一个接近1的值，这样做的好处有：

• 结果随环境影响变化不大，适合用于结构化和非结构化环境
• 不用对每束激光束的所有激光点都计算（只需要对每束光束的端点查表计算概率），计算比较简单

运动畸变成因

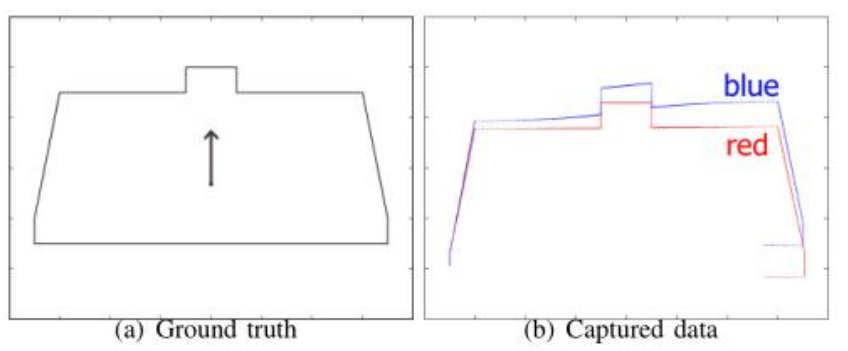
运动畸变如下图所示，观测结果会和真实结果有一个偏差，主要产生的根本原因是我们假设激光雷达的扫描结果是在同一时刻（机器人位姿没有变化）产生，但是实际上激光雷达的扫描结果需要一定时间，在这个时间内机器人如果有运动的话实际的扫描的结果就会出现偏移。假设按照下图场景，激光雷达逆时针旋转，在一开始旋转的时候 $t_0$ 机器人还没有往前走，所以结果是准确的，但是在转过一半之后$(t+\delta t)$机器人已经往前走了一段距离，这个时候激光扫描结果会变小（因为靠近墙了），但是我们还是认为他在$t_0$时刻的位置，所以结果就会显示是墙离我们越来越近了，所以会出现歪掉的现象，原因是因为激光帧率比较低的时候，机器人的运动不能忽略，这个畸变现象是由于运动畸变带来的（根本原因是旋转速度太慢），所以叫做运动畸变。

运动畸变去除

接下来开始介绍怎么进行运动畸变的去除。

纯估计方法

首先讲纯估计的方法，这种方法是一种类ICP的方法。

迭代最近点(ICP)方法

先介绍ICP的方法，ICP(Itrative Cloest Point)迭代最近点的方法的要点是，给定两个两个点云：

$$\begin{aligned} X &= \{x_1, x_2, ..., x_N\}\\ P &= \{p_1, p_2, ..., p_N\} \end{aligned}$$

我们需要找到一个变换关系 $(R, t)$ 使得下式最小，这个过程叫点云配准，或者匹配点云。式子里面有旋转矩阵 $R$ 所以会引入三角量，因此不能用线性最小二乘解来求：

$$E(R, t) = \frac{1}{N}\sum_{i=1}^{N}||x_i-Rp_i-t||^2$$

在给定两个点云的对应点的时候，虽然不能用线性最小二乘解，但是这个式子的最小值有解析解（在后面讲到帧间匹配的时候会推导，这里先直接说明，之后补充），计算过程是：

• 先求出两个点云的几何中心

$$\begin{aligned} u_x &= \sum_{i=1}^{N}x_i\\ u_p &= \sum_{i=1}^{N}p_i \end{aligned}$$

• 对两个点云去中心化

$$\begin{aligned} X' = \{x_i-u_x\} = \{x_i'\}\\ P' = \{p_i-u_p\} = \{p_i'\} \end{aligned}$$

• SVD 分解

$$W = \sum_{i=1}^{N}x_i'p_i'^T = U\begin{bmatrix}\sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\0 & 0 & \sigma_3\end{bmatrix}V^T$$

• ICP 的解是：

$$\begin{aligned} R &= UV^T\\ t &= u_x - Ru_p \end{aligned}$$

实际过程中，我们大概率并不知道对应点关系，这个时候不可以一步计算出 $R$ 和 $t$ 的最佳结果，需要用到期望最大化 (Expectation Maxmization, EM) 的思想，先给定一个初值（匹配关系），利用初值进行计算 R 和 t, 再根据 R 和 t 对点云进行转换，计算误差和新的匹配关系，根据新的匹配关系进项迭代计算，直至最后算出误差小于一个阈值，这个时候可以认为匹配关系和点云之间的转换关系都计算比较准确了，大概过程如下图所示：

VICP方法

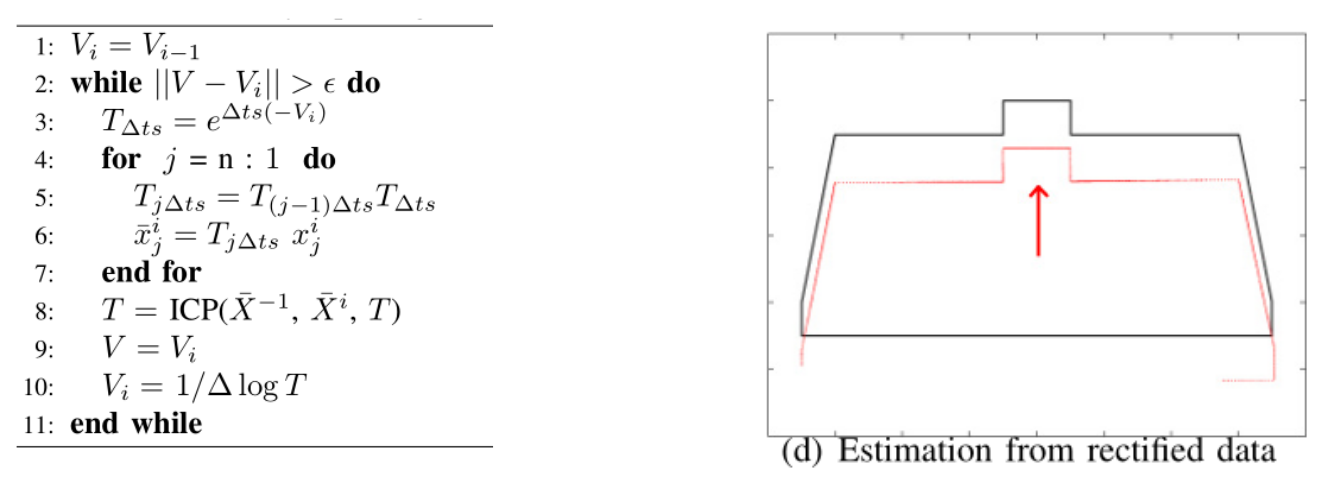
ICP在激光匹配中没有考虑两种情况：激光的运动畸变和部分激光数据可能是错误的（错误数据可能就是来自于运动畸变）。基于这种情况，VICP（Velocity-ICP）把速度的影响也考虑在内，它的要点是假设机器人在扫描过程中进行匀速运动，在匹配迭代的时候同时估计机器人的速度，本质上用匀速运动对一帧内的位姿进行线性插值（LOAM里面也有用到这个方法），具体计算过程如下：

• $X^i, X^{i-1}$ 表示第i帧和第i-1帧的激光扫描数据
• $T^i, T^{i-1}$ 表示对应时刻的位姿
• 机器人的速度$V_i$可以通过两个时刻的位姿和时间差求出
• 我们把第i帧的时间划分为n段，分别是:

$$(t_i-n\Delta t, t_i - (n-1)\Delta t, ... ,t_i - \Delta t, t_i)$$

• 则第i帧的第j个节点的位姿矩阵是：$T_{t_i - (n-j)\Delta t} = T_ie^{(n-j)\Delta t(-V_i)}$
• 所以校正过程是：$\bar X^i = \{e^{(n-j)\Delta t(-V_i)}x_j|j=0,…,n\}$

算法流程和效果如下图所示：

里程计辅助方法

VICP有两个缺点：

• 在用低帧率（5Hz， 200ms）的激光雷达，匀速运动假设不成立（每帧时间太长）
• 在数据预处理（去畸变）的过程中跟状态估计（速度和位姿估计）耦合在一起

而里程计/IMU可以弥补这个缺点，因为它的位姿更新频率很快(200Hz，5ms, IMU能到1kHz)，所以能够更加准确的反应运动情况，同时可以跟状态估计完全解耦。因此在里程计短时间内(200ms)的准确度比较高的时候，我们可以借助里程计来去除畸变，IMU的更新频率也很快，但是它的线性加速度精度太差（控制成本的情况下），所以几乎不能用来估计位置信息。

在处理信息的时候也有两种思路：

• 单片机读取激光雷达数据和位姿信息，进行运动畸变去除，然后上传到CPU，好处是不用考虑不同系统的时间同步问题，但是由于在单片机处理之后再上传所以数据需要压缩，否则会产生延时
• 用CPU读取激光雷达数据，然后单片机上传里程计积分数据，先对数据进行时间同步然后统一进行畸变去除，需要位姿插值，因为没有时延问题所以通常采用这种方法。

接下来介绍具体方法，我们已知的数据有：

• 当前帧激光起始时间：$t_s, t_e$
• (同一帧内)两束激光的时间差$\Delta t$
• 一个包含里程计数据的队列，时间范围应该覆盖当前帧激光的时间范围

接下来具体目标为：

• 获得当前帧激光数据每一个激光束端点的机器人位姿
• 根据求解的位姿把所有激光束转换到统一坐标系下
• 重新封装成一帧激光数据并发布

其中关键步骤就是计算当前帧激光数据的对应机器人位姿：

• 假如里程计数据队列正好对到了激光数据的时间范围（时间同步好了），那么激光帧的起止时间的位姿就是里程计数据队列的队头和队尾数据的时间戳
• 如果开始时间没有对应里程计位姿数据，则用里程计相邻的两个位姿数据进行线性插值（因为里程计数据采集频率高，所以做匀速运动进行线性插值比较合理）
• 在一帧数据之间的任意一点
  • 认为机器人做匀加速运动进行二次插值（用起始点，结束点和中间点）
  • 还可以进行分段线性插值（用激光帧时间范围内的所有里程计数据点进行分段线性插值）

获得每个激光点对应的机器人位姿 $p_i$ 之后，可以将激光点信息 $x_i$（在当前时间插值得到的位姿坐标系下）转换为统一的坐标系下（比如起始时间）：$x_i’=p_i^Tx_i$，接下来重新封装激光信息发布出去：

$$\begin{aligned} x_i' &= (p_x, p_y)\\ range &= \sqrt{p_x^2+p_y^2}\\ angle &= \arctan{(p_y, p_x)} \end{aligned}$$

融合方法

融合方法主要就是考虑前两种的方法的融合。我们先用里程计方法插值得到位姿数据进行去畸变。假设我们认为里程计方法还是存在误差（采集频率还是不够快），我们可以认为误差是跟时间线性分布的，所以我们用ICP的方法进行一次匹配，并将匹配结果作为正确值，这个过程会产生一个误差作为里程计的误差值。基于误差线性分布的假设，我们可以把误差平均分配到每一个时间段内，进行激光点修正，然后再进行ICP迭代直到结果收敛。