本文是我在学习深蓝学院的激光slam课程前端配准第一部分的学习笔记,前面几次基本把数据的预处理讲完了,本次课开始学习 slam 的内容,这次主要是讲了前端配准算法。
无论是激光 slam 还是视觉 slam, 大部分都分成两个部分:前端和后端。其中后端的话各种 slam 都差不多,主要是根据数学公式求解类似 $Ax = b$ 的公式,而不同 slam 方法的前端可以有各种方法。前端总体来说无论是视觉还是激光都是起到一个里程计的作用,本次主要是学习帧间匹配算法中类 ICP 的方法,包括:ICP 匹配方法、PL-ICP 匹配方法、NICP 匹配方法和IMLS-ICP 匹配方法。
ICP 匹配方法
关于原始 ICP 匹配方法算法和原理都在前面的两篇笔记(lidarSLAM 第二次作业和激光雷达运动畸变去除)记录过了,这里不再赘述。
PL-ICP 匹配方法
基本思想
相对于原始的 ICP 算法中用点与点之间的距离作为误差, PL-ICP 是把点到线的距离作为误差。PL-ICP 的基本思想是:激光点是对实际环境中曲面的离散采样,在匹配过程中重要的不是激光点,而是隐藏在激光点中的曲面。这个很好理解,因为在前后两帧激光扫描数据中,我们不一定会准确扫描到上一帧的每个点(这个时候用点和点的距离作为误差就是有问题的),更大可能是扫到了同一个物体(曲面)上的不同点,所以相较于用点对点的距离作为误差,把点到实际曲面的距离作为误差尺度应该是更符合实际的。所以问题就变成了如何恢复曲面。不同算法有不同的恢复方法,PL-ICP 的方法是用分段线性的方法对实际曲面进行近似,以此来定义点到曲面的距离,不同方法的误差表示如下图所示。
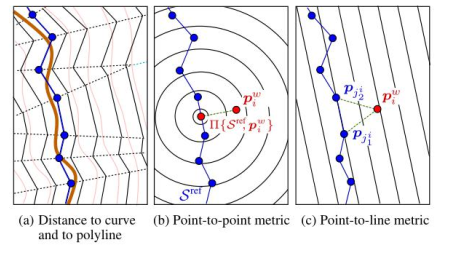
数学描述
我们可以将原始 ICP 算法的目标函数看成以下形式:
其中,
$S^{ref}$ 代表参考激光帧生成曲面上的投影,这里我的理解是由于原始 ICP 没有考虑曲面的影响而是直接匹配每一个点,所以对该点处曲面的投影就是该点,所以对 ICP 而言,$||\mathbf{p}_i \oplus \mathbf{q} - \prod\{S^{ref}, \mathbf{p}_i \oplus \mathbf{q}\}|| = ||\mathbf{p}_i \oplus \mathbf{q} - x_i||, x_i$ 就是匹配点。
然后给定初始解对下式进行迭代:
PL-ICP 目标函数如下:
通过引入了法向量将误差从两个点的距离(差)变成了两点连线在曲面上的法向量的投影,即点到线的距离。
求解过程 & 具体算法
我们的已知数据有:
- 参考激光帧 $y_{t-1}$
- 当前激光帧 $y_t$
- 参考激光帧生成的曲面 $S^{ref}$
- 初始解 $q_o$
需要求解的是两帧激光之间机器人的相对位姿关系 $q^*$
算法过程跟原始 ICP 类似:
- 将当前帧的数据根据初始位姿 $q_k$ 投影到参考帧坐标系下
- 对于当前帧的点 $i$, 在参考帧中找到最近的两个点(因为要连成直线)$(j_1, j_2)$
- 计算直线误差,去除误差过大的点
- 最小化误差函数 $
\sum_{i}(\mathbf{n}^T[\mathbf{R}(\theta)\mathbf{p} + \mathbf{t} - p_{j_1^i}])^2
$
跟 ICP 的区别
首先是误差形式不同,原始 ICP 将点对点的距离作为误差,PL-ICP 对点到线的距离作为误差;
其次两种算法收敛速度不同, ICP 为一阶收敛, PL-ICP 为二阶收敛,速度更快:
PL-ICP 的求解精度更高(更符合实际),尤其是在人工结构化环境中(直线多);
PL-ICP 对初值更敏感,通常要结合里程计一起使用
NICP 匹配方法
NICP 基本思想
相较于前两种 ICP 算法而言,他们都是考虑将距离(点到点,点到线)作为误差尺度, NICP 更关注面与面(2d 里是线与线)的误差;因此它还利用实际曲面的特征来对错误匹配点进行过滤,主要考虑的参数为法向量和曲率;因此在误差项里除了考虑对应点的欧氏距离以外,还考虑对应点法向量的角度差。
NICP 数学描述
首先有以下变量:
$p_i$ 表示激光点坐标 $(x, y, z)$
$n_i$ 表示对应点的法向量
$\sigma_i$ 对应点曲率
$\tilde{p}_i = (p_i, n_i)^T$ 为扩展点(坐标加法向量)
$T$ 表示欧式变换矩阵
$\oplus$ 对于 $\tilde{p}$ 的操作符(对于法向量只需要考虑旋转):
则 NICP 的误差函数定义为:
目标函数为:
其中,$\tilde{\Omega}_{ij}$ 为信息矩阵(表示权重):
法向量和曲率的计算
先找到点 $p_i$ 周围半径 $R$ 范围内的所有点 $V_i$,然后计算均值和方差
然后对方差进行特征分解(2维情况下),用类似于 PCA (主成分分析)的方法找出这堆点对应曲面的曲率和法向量:
对曲率的定义为: $\sigma_i = \frac{\lambda_1}{\lambda_1 + \lambda_2}$
对法向量的定义为:最小特征值对应的特征向量
对点进行过滤
如果没有 well-define 的法向量(杂点),拒绝匹配该点
两点间距离大于阈值,拒绝: $||p_i^c - T\oplus p_j^r|| > \epsilon_d$
两点曲率之差大于阈值,拒绝: $|\log{\sigma_i^c}-\log{\sigma_j^r}| > \epsilon_\sigma$
两点法向量角度之差,拒绝: $\mathbf{n}_i^c\mathbf{T}\oplus\mathbf{n}_j^r < \epsilon_n$
目标函数求解
目标函数为:
没办法求解析解,只能通过 LM 求解,具体求解方法后面讲优化的时候具体讲解。
NICP 总结
由于在寻找点匹配过程中考虑了法向量和曲率,可以提前排除一些错误的匹配;在开源领域是效果最好的匹配方法。
具体算法流程为:
计算参考激光帧和当前激光帧中每一个点的法向量和曲率(通过特征分解)。
根据当前解,把当前激光帧的点转换到参考坐标系中,并且根据欧式距离、法向量、曲率等信息来选择匹配点(也有可能没有匹配点)。
根据上面介绍的方法,用LM方法进行迭代求解,迭代收敛即可得到两帧激光数据之间的相对位姿。
IMLS-ICP 匹配方法 (Implicit Moving Least Square)
IMLS-ICP 基本思想
跟前面两种方法一样,还是考虑从点云重建曲面,重要的是怎么重建平面使其更符合实际; IMLS-ICP 的思想是选择具有代表性的激光点来进行匹配,既能减少计算量同时又能减少激光点分布不均匀导致的计算结果出现偏移(在3d情况下尤其重要,因为点太多了)。
代表点选取
具有丰富特征的点,即为结构化的点:具有良好的曲率和法向量的定义。
曲率越小的点越好,因为曲率为0代表着直线,代表着最结构化的点,也代表着具有非常好的法向量定义,能够提供足够的约束。
选点的时候需要注意选取的激光点的均衡以保证可观性,因为是平面匹配,不存在角度不可观的情况。只需要考虑X方向和Y方向的可观性。要保证两者的约束基本上是一致的,才能让结果不出现偏移。
曲面重建
已知点云集合 $P_k$ 中每一个点 $p_i$ 的法向量 $n_i$ , 则 $P_k$ 中隐藏的曲面为:
其中,
$I^{P_k}(x) = 0$ 对应的集合表示曲面,空间中点到曲面的距离代入方程计算即可,证明过程看参考文献 Provably good moving least square。
匹配求解
- 当前帧中一点 $x_i$ 到曲面的距离为$I^{P_k}(x_i)$
- $P_k$ 中离点 $x_i$ 最近点的法向量为 $n_i$
- 点 $x_i$ 在曲面的投影为:$y_i = x_i - I^{P_k}(x_i)n_i$
- 点 $x_i$ 和 点 $y_i$ 为对应的匹配点,求解误差: $\sum((Rx_i + t - y_i)n_i)^2$